Польза геометрии в жизни человека
Муниципальное автономное общеобразовательное учреждение
«Средняя общеобразовательная школа № 84»
РЕФЕРАТ
на тему ЗНАЧЕНИЕ ГЕОМЕТРИИ В ЖИЗНИ ЛЮДЕЙ
Выполнила:
ученица 9«Б» класса
Русакова Лидия
Руководитель:
учитель математики
Сивцева Ольга Николаевна
Пермь 2011
Содержание.
Введение. Актуальность………………………………….……….……………..3
1. История возникновения геометрии………………….………….……………4
2. Значение геометрии в XXI веке …………………………………………….5
3. Профессии, связанные с геометрией. ………….………….…………………6
3.1. Архитектор…………………………………………………………………..
3.2. Инженер……………………………………………………………………..
3.3. Дизайнер……………………………………………………………………
3.4. Конструктор………………………………………………………………..
3.5. Модельер……………………………………………………………………
3.6. Психолог…………………………………………………………………….
Заключение ……………………………………………………….………………8
Список литературы ………………………………………………..……………9
Приложения…………………………………………………………………………..10
Введение. Актуальность.
Геоме́трия (от γη — Земля и μετρεω — мера, измерение) — наука о пространстве, точнее — наука о формах, размерах и границах тех частей пространства, которые в нем занимают вещественные тела; раздел математики, изучающий пространственные отношения и их обобщения (ru.wikipedia.org/wiki/Геометрия).
В общеобразовательной школе предмет «Геометрия» изучается с 7 класса и, по мнению многих учащихся, является одним из сложнейших школьных предметов. Многие учащиеся не понимают назначения геометрии в жизни, так как не собираются связывать свою будущую профессию с математикой вообще.
Я учусь в 9 классе, и уже сейчас передо мной и моими одноклассниками стоит вопрос выбора профессии. Во время беседы со своими сверстниками, я узнала, что многие из них хотели бы в будущем заниматься банковским делом, экономикой, психологией, медициной, дизайном одежды. Передо мной встал вопрос: неужели профессии, в которых нужна геометрия никто не выбирает, разве жизнь без знаний геометрии не изменилась бы, и вообще нужна ли геометрия в жизни людей?
Чтобы дать подробный ответ на данный вопрос, я поставила перед собой ряд задач:
- на основе изучения литературы и Интернет-ресурсов найти точки соприкосновения между геометрией и практической действительностью;
- изучить профессии напрямую связанные с геометрией.
1. История возникновения геометрии.
Геометрия возникла давно, это одна из самых древних наук. Родиной геометрии считают обыкновенно Вавилон и Египет. Греческие писатели единодушно сходятся на том, что геометрия возникла в Египте и оттуда перенесена в Элладу. Первые шаги культуры всюду, где она возникала, в Китае, в Индии, в Ассирии, в Египте, были связаны с необходимостью измерять расстояния и участки на земле, объемы и веса материалов, продуктов, товаров; первые значительные сооружения требовали нивелирования, выдержанной вертикали, знакомства с планом и перспективой.
Важную роль играли и эстетические потребности людей: желание украсить свои жилища и одежду, рисовать картины окружающей жизни. Все это способствовало формированию и накоплению геометрических сведений. За несколько столетий до нашей эры в Вавилоне, Китае, Египте и Греции уже существовали начальные геометрические знания, которые добывались в основном опытным путем. Но они не были еще систематизированы и передавались от поколения к поколению в виде правил и рецептов, например, правил нахождения площадей фигур, объемов тел, построение прямых углов и т.д. Не было еще доказательств этих правил, и их изложение не представляло собой научной теории.
Необходимость измерять промежутки времени требовала систематического наблюдения над движением светил, а, следовательно, измерения углов. Таким образом, были сконструированы солнечные часы (Приложение 1). Всё это было неосуществимо без знакомства с элементами геометрии, и во всех названных странах основные геометрические представления возникали частью независимо друг от друга, частью — в порядке преемственной передачи.
Еще в древности возникла потребность перевозки. Тогда, в Бронзовом веке (3500–1000 до н.э.), изобрели первое колесо.
Колесо – круглый, свободно вращающийся или закреплённый на оси диск. Это одно из самых важных изобретений в области механики и геометрии за всю историю человечества.
Постоянно имея дело с поваленными деревьями и бревнами, человек обнаружил, что они могут катиться. Оказывается, то самое бревно, которое он с товарищами едва мог перенести на несколько метров, могло катиться само, если, конечно, его подтолкнуть (Приложение 2).
Первое использование колеса не в транспортном средстве, а в механизме совсем иного назначения – гончарном круге – относится тоже к Бронзовому веку. Судя по археологическим находкам, это было просто тележное колесо, приспособленное для изготовления посуды. Глиняную посуду формовали в Древнем Египте уже около 3000 до н.э. – сначала на медленно вращающихся кругах, а спустя несколько столетий – и на быстрых, от чего возросло разнообразие их форм и улучшилось качество.
2. Значение геометрии в XXI веке.
Великий французский архитектор Корбюзье как-то воскликнул: «Все вокруг геометрия!». Сегодня уже в начале XXI столетия мы можем повторить это восклицание с еще большим изумлением. В самом деле, посмотрите вокруг — всюду геометрия! Современные здания и космические станции, авиалайнеры и подводные лодки, интерьеры квартир и бытовая техника – все имеет геометрическую форму. Геометрические знания являются сегодня профессионально значимыми для многих современных специальностей: для дизайнеров и конструкторов, для рабочих и ученых. И уже этого достаточно, чтобы ответить на вопрос: «Нужна ли нам Геометрия?»
Во-первых, геометрия является первичным видом интеллектуальной деятельности, как для всего человечества, так и для отдельного человека. Мировая наука начиналась с геометрии. Ребенок, еще не научившийся говорить, познает геометрические свойства окружающего мира. Многие достижения древних геометров (Архимед, Аполлоний) вызывают изумление у современных ученых, и это несмотря на то, что у них полностью отсутствовал алгебраический аппарат.
Во-вторых, геометрия является одной составляющей общечеловеческой культуры. Некоторые теоремы геометрии являются одними из древнейших памятников мировой культуры. Человек не может по-настоящему развиться культурно и духовно, если он не изучал в школе геометрию; геометрия возникла не только из практических, но и из духовных потребностей человека.
Основой курса геометрии является принцип доказательности всех утверждений. И это единственный школьный предмет, включая даже предметы математического цикла, полностью основанный на последовательном выводе всех утверждений. Людьми, понимающими, что такое доказательство, трудно и даже невозможно манипулировать.
Итак, Геометрия — один из важнейших предметов, причем не только среди предметов математического цикла, но и вообще среди всех школьных предметов. Ее целевой потенциал охватывает необычайно широкий арсенал, включает в себя чуть ли не все мыслимые цели образования.
3. Профессии, связанные с геометрией.
Конечно, математика нужна нам везде: в магазине, в автобусе, в школе и дома. Однако, как правило, профессии, где нужна только геометрия, в жизни не встречаются.
3.1.. Архитектор.
На мой взгляд, самая “геометрическая профессия” – архитектор. Архитектура (Приложение 3) – одна из наиболее всеобъемлющих областей человеческой деятельности, занимающаяся организацией пространства и времени и решающая любые пространственные и временные задачи, от разработки стратегий развития агломераций до дизайна дверных ручек. Архитектор придумывает основную концепцию здания, его облик, увязывает воедино все нюансы. Задача архитектора — спроектировать сооружение, максимально отвечающее потребностям заказчика.
3.2. Инженер.
Еще одна немаловажная профессия – инженер. Инженер-строитель – это производитель работ, т.е. прораб, он руководит общестроительными работами, монтажом конструкций, осуществляет контроль за качеством.
В проектных организациях инженеры выполняют работы по комплексному проектированию: архитектурной, конструктивной части (электроснабжение, отопление и вентиляция, водопровод и канализация, слаботочные системы — телефон, пожарная сигнализация, теленаблюдение и др.). Кроме того, разрабатывают генеральные планы проектируемых комплексов, куда входят дороги, земляные работы, организация строительства. Направление деятельности строителей очень широкое — кроме возведения зданий, производственных комплексов, фабрик, они проектируют мосты, гидротехнические сооружения, плотины, дамбы и т. д.
3.3. Дизайнер.
Дизайн – это творческая деятельность, целью которой является определение формальных качеств промышленных изделий. Эти качества включают и внешние черты изделия, но главным образом те структурные и функциональные взаимосвязи, которые превращают изделие в единое целое, как с точки зрения потребителя, так и с точки зрения изготовителя (Приложение 4). Быть дизайнером это означает быть творческой личностью в определенной области. Для этого те, кто решил выбрать эту профессию, отправляются на специальные курсы подготовки, куда обязательно будут входить изучение черчения, геометрии и других специальных программ, которые пригодятся будущему специалисту.
3.4. Конструктор.
Конструктор осуществляет конструкторское и технологическое проектирование, разрабатывает и внедряет инновационные технологические процессы производства, разрабатывает технологические конструкции различного назначения, отдельные их элементы и части, цехи. Проводит исследования в области конструирования с использованием новых разработок, достижений различных областей науки. Для того, чтобы стать конструктором необходимо изучать технику, механику, физику, алгебру, геометрию, химию… Личные качества: высокая концентрация и устойчивость внимания, логика, технический склад ума, аналитическое мышление. 3.5. Модельер. | |
|
Заключение.
Значение геометрии огромно. Во-первых, все, что нас окружает, имеет геометрическую форму: микроволновая печь, глобус, шкатулка и многое другое. Во-вторых, люди, умеющие рассуждать и доказывать, могут самостоятельно находить выход из коварных жизненных ситуаций. Их трудно обмануть.
Геометрия встречается во многих профессиях, без которых человечество не смогло обойтись. Например, перед тем как построить жилое здание, люди проектируют будущую постройку на чертежах в уменьшенном масштабе. Этим занимается архитектор. Тот, кто руководит общестроительными работами и осуществляет контроль за качеством называется инженером-строителем. Конструктор разрабатывает элементы, части технологических конструкций. Для того чтобы стать конструктором, необходимо сначала выучить множество наук, среди которых присутствует геометрия. С помощью модельера наши вещи становятся более удобными, стильными и качественными. Его задача изготавливать новые модели одежды, определять общее конструктивное решение, придумывать различные дополнения. Психолог с помощью психогеометрии быстро и точно нарисует психологический портрет испытуемого, узнает, какие черты его характера являются главными, а какие – второстепенными, а также поможет понять, с кем человеку сложнее всего взаимодействовать.
А если на минуту представить, что геометрии не существует и ни один человек не подозревает о наличие геометрии, то неужели люди до сих пор жили бы в пещерах, ходили на охоту и одевались в шкуры животных?
Из сказанного выше можно сделать вывод, что если бы люди не начали изучать геометрию, то прогресс и множество современных изобретений дались бы человечеству с большим трудом и возможно гораздо позже.
Список литературы.
- Атанасян Л.С., Бутузов В. Ф. и др. Геометрия 7-9: учебник. – М.: Просвещение, 2008 г.
- Глейзер Г.И. История математики в школе: Пособие для учителей. – М.: Просвещение, 1981 г.
- Комацу М. Многообразие геометрии. – М.: Знание, 1981 г.
- Кордемский Б.А. Великие жизни в математике. – М.: Просвещение, 1995 г.
- ru.wikipedia.org/wiki/Геометрия
- https://www.coolreferat.com/История_Геометрии
- http//www.shevkin.ru/?action=Page&ID=232
ПРИЛОЖЕНИЯ
Приложение 1
Приложение 2
Приложение 3
Приложение 4
Приложение 5
Источник
В школе мы несколько лет подряд прилежно изучаем геометрию. Но не зря ли мы тратим время? Чем может помочь геометрия в жизни? Измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться.
Вешаем зеркало
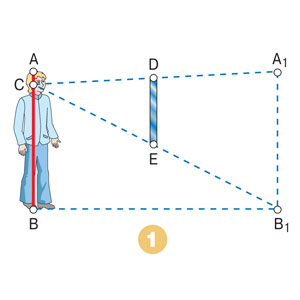
Вы решили повесить в прихожей зеркало. Тут же возникает вопрос: какой минимальной высоты должно быть зеркало, чтобы человек среднего роста мог видеть себя в нём целиком? И ещё: имеет ли при этом значение размер помещения, где будет висеть зеркало? Решение. Предмет и его отражение симметричны относительно плоскости зеркала. Построим в нём изображение человека (рис. 1): АВ — человек, А1В1 — его изображение, точка С — глаз, DE — зеркало. Из рисунка видно, что минимальная высота зеркала приблизительно равна половине роста человека, считая от уровня глаз. При этом высота Е нижнего края зеркала от пола должна быть вдвое меньше расстояния от пола до глаз. Легко понять, что, на каком бы расстоянии от такого зеркала ни находился человек, он сможет увидеть себя в нём с головы до ног, значит, размер помещения значения не имеет.
Завариваем чай
Перед вами стеклянные чайники четырёх моделей одинаковой вместимости (рис. 2). В каком чайнике заваренный чай останется тёплым дольше? Решение. Из курса физики известно, что время охлаждения пропорционально площади поверхности тела. Значит, чем меньше поверхность чайника, тем дольше остывает чай. Самая маленькая площадь поверхности у четвёртого чайника, так как его форма близка к сфере (S = d2).
Выдерживаем прямые углы
Если вы решили склеить коробку, сделать шкатулку или выложить плитку, важно, чтобы все детали были точными прямоугольниками или квадратами. В противном случае всё пойдёт наперекосяк. Как проверить, имеет ли деталь нужную «геометрию»? Решение. Чтобы проверить, у всех ли деталей, с которыми вы работаете, прямые углы и одинаковые линейные размеры, можно использовать строи-тельный угольник (рис. 3), а можно применить знания по геометрии. Убедитесь в том, что противоположные стороны четырёхугольника равны и при этом диагонали тоже имеют одинаковую длину. Как вы и сами знаете, сделать это можно с помощью линейки. Но вот вопрос: обязательно ли проверять и стороны и диагонали? Геометрия утверждает, что да! Например, на рис. 4 диагонали в четырёхугольнике слева равны, но очевидно, что его углы совсем не прямые. А в четырёхугольнике справа противоположные стороны равны, но это тоже не прямоугольник. Для проверки прямоугольности геометрия ещё советует убедиться в равенстве всех четырёх отрезков, на которые разбиваются диагонали в точке их пересечения.
Строим прямой угол на земле
Известен старинный способ постро-ения прямого угла на поверхности земли. Его использовали ещё древние египтяне. Они строили прямой угол с помощью обычной верёвки, на которой через равные расстояния завязаны тринадцать узелков. Чтобы отрезки на верёвке были одинаковые, узелки завязывали вокруг колышков, вбитых в землю на равном расстоянии друг от друга. В чём состоит этот «верёвочный» способ? Решение. В древности при закладке храма такую верёвку с узелками использовали для определения направлений его стен. Концы верёвки на месте крайних узелков связывали, а затем натягивали её на три колышка так, как показано на рис. 5. Стороны при этом имели соотношение 3:4:5. В таком треугольнике один из углов получается прямым. Впоследствии этот факт был доказан в теореме Пифагора. Поэтому первых геометров называли ещё «натягивателями верёвок». Нужно отметить, что таким способом построения прямого угла на местности пользуются и сегодня, например при закладке фундамента небольшого строения.
Проверяем перпендикулярность стен
Как проверить, перпендикулярны ли друг другу соседние стены в комнате, воспользовавшись верёвкой с узелками из предыдущей задачи? Решение. Если предположить, что стены в комнате вертикальны, а пол горизонтален, то проверку проводят так. От точки на полу в углу между стенами откладывают отрезки длиной 3 и 4 единицы (рис. 6). Если стены перпендикулярны, то расстояние между концами отрезков будет равно 5 единицам, так как построенный тре-угольник со сторонами 3, 4, 5 — прямоугольный.
Отмеряем нужный объём
Часто в рецептуре того или иного блюда требуется взять четверть (или половину) стакана жидкости, муки либо какого-либо другого продукта. Как отмерить такой объём с наибольшей точностью, не прибегая к дополнительным измерительным средствам? Решение. Воспользуемся стаканом цилиндрической формы — это важно для точности измерений. Чтобы отмерить четверть стакана жидкости, надо из наполненного стакана вылить столько, чтобы оставшаяся в нём жидкость закрыла половину дна (рис. 7). Она займёт примерно четверть объёма стакана-цилиндра. Аналогично поступаем, если надо отмерить половину стакана. Наклоняем стакан так, чтобы оставшаяся в нём жидкость закрыла всё дно (рис. 8). А можно ли геометрическим способом узнать объём бутылки? Конечно! Для этого надо заполнить бутылку водой чуть меньше чем наполовину (рис. 9, слева) и измерить объём воды, умножив площадь дна бутылки на высоту налитой в неё воды (напомним, что объём цилиндра вычисляется как произведение площади основания на высоту). Затем нужно перевернуть бутылку горлышком вниз так, чтобы вода не вытекла, и измерить объём верхней цилиндрической части бутылки, оставшейся пустой (рис. 9, справа). Полный объём бутылки равен сумме найденных объёмов. Для точности можно учесть толщину стенок бутылки.
Укрепляем калитку
Прямоугольная калитка (рис. 10, слева) со временем расшатывается и становится похожей на параллело-грамм. Этого можно избежать, прибив к ней ещё одну планку. Только надо знать, как это сделать. Решение. Выбор такого положения планки, как показано на рис. 10, справа, основан на свойстве жёсткости треугольника. Оно гласит: существует единственный треугольник с заданными длинами сторон. Планка и есть гипотенуза такого треугольника.
Выбираем табурет
Если вы решили предыдущую задачу, то без труда определите, на какой табурет (рис. 11) можно сесть без риска оказаться на полу. Решение. Безопасный табурет изображён на правой картинке, так как его сиденье и ножки образуют треугольник.
Исправляем ошибку кроя
Предположим, вам нужно вырезать для аппликации два разносторонних треугольника из цветной бумаги — «левый» и «правый». Вы случайно вырезали их одинаковыми — оба «левые». Можно ли, не используя новый кусок бумаги, исправить ошибку? Решение. Для исправления ошибки вы можете разрезать один из треугольников, например так, как показано на рис. 12, а затем сложить из него нужный треугольник.
Находим середину
Как без всяких измерений найти середину негнущегося прута, доски или металлического стержня? Решение. Можно отмерить размеры стержня на шнуре, затем сложить его пополам и отложить полученную длину. А можно воспользоваться геометрическим построением середины отрезка с помощью циркуля и линейки, если, конечно, размеры позволяют это сделать. Ещё более рациональное решение даёт физика. Середину однородного стержня легко найти, используя понятие центра тяжести (рис. 13).
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
‹
›
Источник
