Польза от резонанса в трансформаторе
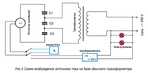
Группа разработчиков на Смоленщине. Они использовали принцип описанной выше конденсаторной установки. Примерная схема устройства приведена на рис.5. Здесь также от источника колебательной энергии подаётся ток на три последовательно соединённые конденсатора С1, С2, С3. Заряд их пластин колеблется в такт источника раскачки колебаний, но С2 включён схемой в цепь высоковольтной обмотки бытового трансформатора в виде колебательного контура. Естественно, колебательный контур С2 с обмоткой трансформатора воспринимает “маленькие порции” раскачки, и уже сам собой, в результате резонанса с эфиром, начинает выдавать необходимую мощность во вторичную обмотку на полезную нагрузку ~ 220 V. Схема предельно простая, это надо отдать должное “сообразительности” смоленских “парней”. Здесь сравнительно небольшой раскачки источника колебаний вполне хватает для резонансного возбуждения силовых колебаний тока в данном контуре, а с вторичной обмотки трансформатора можно спокойно снимать трансформированный ток на любую полезную нагрузку. Возможно, что сам Тесла использовал этот приём для привода своего электромобиля в движение, недаром же он покупал радиолампы в магазине, которые и являлись источником колебательной энергии для обкладок конденсаторов, а индуктивность статорной обмотки тягового электродвигателя служила основной частью колебательного контура – источника тока (вместо первичной обмотки трансформатора в схеме рис.5). А сейчас поговорим о главном – о величине мощности раскачки эфира вокруг ёмкостей и индуктивностей с целью получения свободной энергии (реактивной мощности), поисками которой заняты специалисты во всём техническом мире. Сначала рассмотрим теоретическую сторону вопроса.
Поскольку формула реактивной мощности для любой обмотки Q = I^2*2П*F* L,
где I -величина тока, F – частота тока, L- индуктивность. Величина L задана геометрией обмотки трансформатора или контура, её изменять трудновато, но её и использовал Капанадзе. Другая величина – частота F может изменяться. В реактивной мощности она задаётся частотой электростанции (источником колебаний), но с увеличением её увеличивается мощность свободной энергии, значит, разумно её повышать при раскачке индуктивности. А раскачать индуктивность по частоте, для получения и повышения тока I необходим конденсатор, подключённый к индуктивности. Но, чтобы начать раскачку контура, нужен первоначальный импульс тока. А его сила, в свою очередь, зависит от активного сопротивления самой обмотки, сопротивления соединительных проводов и, как не удивительно, волнового сопротивления этой цепочки тока. Для постоянного тока этого параметра не существует, а для переменного обязательно возникает и ограничивает наши возможности, а с другой стороны помогает нам. Из уравнений длинных линий связи известно,-волновое сопротивление движения для любой электромагнитной волны по проводам должно быть согласовано с сопротивлением нагрузки в конце линии. Чем лучше согласование, тем экономичнее устройство. В контурах, состоящих из ёмкости и индуктивности, из которых состоит “тесловка”, волновое сопротивление определяется величиной которая, если её поделить на активное сопротивление проводников, в принципе, является добротностью контура, т.е. числом, показывающим во сколько раз напряжение в катушке контура возрастает по отношению к задающему напряжению от генератора электростанции (источника раскачки).
Zв = КОРЕНЬ ( L / С ),
Вот этим принципом и пользовался Тесла, изготавливая катушки всё более солидные по размеру, т. е. увеличивая, и увеличивая L – индукцию катушки и чисто интуитивно стремился к волновому числу Zв = 377 Ом. А это и есть волновое сопротивление не чего нибудь, а обыкновенного эфира по Максвеллу, хотя его конкретную величину определили позднее исходя из условий распространения электромагнитных волн в атмосфере и космосе. Приближение к этому числу волнового сопротивления уменьшает мощность раскачки. Отсюда всегда можно хотя бы приблизительно вычислить даже частоту колебаний самого эфира, при которой требуется минимальная энергия раскачки от электростанции для “тесловки” вырабатывающей реактивную энергию, но это отдельная тема рассмотрения.
В будущем видится предельно простой генератор тока для любых мощностей. Это трансформатор приемлемой мощности, первичная обмотка которого подсоединяется через рассчитанный конденсатор (с соответствующей реактивной мощностью) к источнику электрической раскачки сравнительно небольшой мощности, работающего при запуске от аккумулятора. Вторичная обмотка трансформатора через выпрямитель и инвертор выдаёт в расходную сеть необходимый ток с частотой 50 Герц для потребителей и одновременно питает, минуя аккумуляторы, схему раскачки, точнее сам себя (по рис.5.). Сейчас это кажется нереальным в силу закона сохранения энергии, поскольку не учитывается действие эфира, однако в ближайшем будущем такие установки будут широко распространёнными в быту и на производствах. Реактивная мощность, точнее свободная энергия эфира, подчеркнём, эфира Максвелла и Кельвина, должна и будет работать на людей в полной мере, как это предсказывал великий Никола Тесла. Время, которое он предвидел, уже наступило благодаря воспитанной промышленностью громадной армии специалистов электриков и интернету, позволяющему обмениваться мировым опытом.
https://kapagen.livejournal.com/2342.html
Серия сообщений “Изобретения”:
Часть 1 – Любой бензин из отходов
Часть 2 – Изобрёл велосипед
Часть 3 – Резонансный трансформатор – энергия из эфира.
Часть 4 – Электромобилю зеленый свет!
Часть 5 – Solar Impulse завершил перелет через США
…
Часть 44 – ЛЕВИТИРУЮЩИЙ ДВИГАТЕЛЬ
Часть 45 – Подземный транспорт прошлого, настоящего и будущего.
Часть 46 – Как изготавливали механизмы в древности.
Источник
Знакомство с трансформатором Н. Тесла.
Новомодный феномен резонансного трансформатора Николы Тесла возник не давно, а Интернет забит фотографиями и интригующими видеосъемками молний и коронарных разрядов.
Вспомним, что трансформатор первоначально был предназначен не для показательного выступления в цирке, а для передачи радиосигналов на далекие расстояния. В связи с этим предлагаю ознакомиться с его принципом работы и найти ему практическое применение.
Трансформатор Тесла состоит из двух основных частей, см. рис.1а;
1. Генерирующей части, состоящей из высоковольтного источника питания, накопительного конденсатора С1, разрядника и катушки связи L1. Частота генерации зависит от напряжения питания, емкости конденсатора С1, характеризующее время разряда, а так же промежутком между электродами разрядника;
2. Резонансной катушки индуктивности L2, заземления и сферы, см. рис. 1а.
Если вглядеться в схему этого трансформатора внимательнее, то мы увидим известную схему последовательного колебательного контура, состоящего из катушки индуктивности L2 с открытой емкостью С, образованной между сферой и землей. Это открытый колебательный контур, который был открыт Дж. К. Максвеллом.
Обратимся к классической теории принципа действия открытого колебательного контура:
Как известно колебательный контур состоит из катушки индуктивности и конденсатора. Исследуем простейший колебательный контур, катушка которого состоит из одного витка, а конденсатор представляет собой две рядом расположенные металлические пластины. Подадим в разрыв индуктивности контура 1 переменное напряжение от генератора, см. рис.2а. В витке потечет переменный ток и создаст вокруг проводника магнитное поле. Это сможет подтвердить магнитный индикатор в виде витка, нагруженного лампочкой. Для того, что бы получить открытый колебательный контур, раздвинем пластины конденсатора. Мы наблюдаем, что лампа индикатора магнитного поля продолжает гореть. Чтобы лучше понять, что происходит в данном опыте, смотри рис. 2а. По витку контура 1 течёт ток проводимости, который вокруг себя создает магнитное поле Н, а между пластинами конденсатора – равный ему, так называемый, ток смещения. Несмотря на то, что между пластинами конденсатора нет тока проводимости, опыт показывает, что ток смещения создаёт такое же магнитное поле, как и ток проводимости. Первым, кто об этом догадался, был великий английский физик Дж. К. Максвелл.
В 60-х годах 19-го столетия, формулируя систему уравнений для описания электромагнитных явлений, Дж. К. Максвелл столкнулся с тем, что уравнение для магнитного поля постоянного тока и уравнение сохранения электрических зарядов переменных полей (уравнение непрерывности) несовместимы. Чтобы устранить противоречие, Максвелл, не имея на то никаких экспериментальных данных, постулировал, что магнитное поле порождается не только движением зарядов, но и изменением электрического поля, подобно тому, как электрическое поле порождается не только зарядами, но и изменением магнитного поля. Величину где — электрическая индукция, которую он добавил к плотности тока проводимости, Максвелл назвал током смещения. У электромагнитной индукции появился магнитоэлектрический аналог, а уравнения поля обрели замечательную симметрию. Так, умозрительно был открыт один из фундаментальнейших законов природы, следствием которого является существование электромагнитных волн. В последствии Г.Герц опираясь на эту теорию доказал, что электромагнитное поле излучаемое электрическим вибратором равно полю излучаемое емкостным излучателем.
Раз так, убедимся еще раз, что происходит, когда закрытый колебательный контур превращается в открытый и как можно обнаружить электрическое поле Е ? Для этого рядом с колебательным контуром поместим индикатор электрического поля, это вибратор, в разрыв которого включена лампа накаливания, она пока не горит. Постепенно раскрываем контур, и мы наблюдаем, что лампа индикатора электрического поля загорается, рис. 2б. Электрическое поле теперь не сосредоточено между пластинами конденсатора, его силовые линии идут от одной пластины к другой через открытое пространство. Таким образом, мы имеем экспериментальное подтверждение утверждения Дж. К. Максвелла, что емкостной излучатель порождает электромагнитную волну. Никола Тесла обратил на этот факт внимание, что при помощи совсем не больших излучателей можно создать достаточно эффективный прибор для излучения электромагнитной волны. Так родился резонансный трансформатор Н. Тесла. Проверим и этот факт, для чего вновь рассмотрим назначение деталей трансформатора.
И так, сфера и заземление выполняют роль пластин открытого конденсатора. Геометрические размеры сферы и технические данные катушки индуктивности определяют частоту последовательного резонанса, которая должна совпадать с частотой генерации разрядника.
Иными словами, режим последовательного резонанса позволяет трансформатору Тесла достигать таких величин напряжений, что на поверхности сферы появляется коронарный разряд и даже молнии. Весь фокус состоит в том, что коэффициент трансформации резонансного трансформатора выше соотношения витков катушек L1/L2 и значительно выше, чем в трансформаторах с ферро сердечниками. Здесь индуктивность L2, сфера и заземление, представляют из себя открытый резонансный колебательный контур. Именно по этому трансформатор Тесла называется резонансным.
Рассмотрим работу трансформатора Тесла, как последовательный колебательный контур:
— Этот контур необходимо рассматривать как обычный LC – элемент, рис. 1а.б, а так же рис. 2а, где включены последовательно индуктивность L, открытый конденсатор С и сопротивление среды Rср. Угол сдвига фаз в последовательном колебательном контуре между напряжением и током равен нулю (φ=0), если ХL = — Хс, т.е. изменения тока и напряжения в нем происходят синфазно. Это явление называется резонансом напряжений (последовательным резонансом). Следует отметить, что при понижении частоты от резонанса, ток в контуре уменьшается, а резонанс тока несет емкостной характер. При дальнейшей расстройке контура и понижении тока на 0,707, его фаза смещается на 45 градусов. При расстройке контура вверх по частоте, он приобретает индуктивный характер. Это явление часто используют в фазоинверторах.
Если мы рассмотрим схему изображенную на рис. 3, то мы сможем предоставить простые расчеты, из которых видно, что напряжение на пластинах излучателя вычисляется исходя из добротности контура Q, которая реально может находиться в пределах 20 – 50 и много выше.
Где полоса пропускания определяется добротностью контура:
Δf=fo/Q;
Тогда напряжение на пластинах излучателя будет выглядеть согласно следующей формуле:
U2= Q * U1.
В таблице 1 расчетные данные приведены для частоты 7.0 МГц не случайно, это дает возможность любому желающему коротковолновику провести радиолюбительский эксперимент в эфире. Здесь входное напряжение U1 условно взято за 100 Вольт, а добротность за 26.
Таблица 1.
f ( МГц) | L (мкГн) | ХL (Ом) | C (пФ) | — Xc (Ом) | Δf (кГц) | Q | U 1/U 2 (В.) |
7 | 30,4 | 1360 | 17 | 1340 | 270 | 26 | 100/2600 |
Напряжение U2 согласно расчетам составляет 2600В, что подтверждается практической работой трансформатора Тесла. Данное утверждение приемлемо в тех случаях, когда отсутствует изменение частоты или сопротивления нагрузки данного контура. В трансформаторе Н. Тесла оба фактора постоянны.
Полоса пропускания трансформатора Тесла зависит от нагрузки, т.е., чем выше связь открытого конденсатора С (сфера-земля) со средой, тем больше нагружен контур, тем шире его полоса пропускания. Тоже происходит с контуром, нагруженным активной нагрузкой. Таким образом, площадь пластин излучателя антенны определяет его емкость С и соответственно диктует ширину полосы пропускания. Тем не менее, здесь нужно понимать, что чрезмерное увеличение полосы пропускания за счет увеличения объема излучателей приведет к снижению добротности контура и соответственно приведет к уменьшению эффективности резонансного трансформатора и всего устройства в целом.
Подводя итог, мы приходим к выводу, что излучает не индуктивность трансформатора Тесла L2, а элементы открытого конденсатора (сфера-земля рис. 1а.) являющегося частью резонансной системы. Это емкостной излучатель с двумя полюсами, который создает вокруг себя мощное и концентрированное электромагнитное излучение. Трансформатор Тесла обладает особенностью накопления энергии, что характерно только последовательному LC – контуру, где суммарное выходное напряжение значительно превосходит входное, что наглядно видно из результатов таблицы. Данное свойство давно практикуют в промышленных радиоустройствах для повышения напряжения в устройствах с большим входным сопротивлением.
Таким образом, мы можем сделать следующий вывод:
Трансформатор Тесла, это высокодобротный последовательный колебательный контур, где сфера является открытым элементом, осуществляющим связь со средой. Индуктивность L является лишь закрытым элементом и резонансным трансформатором напряжения не участвующим в излучении.
Далее в тексте, будет удобно называть емкостной излучатель диполем Тесла. Это вполне справедливо, ведь «диполь» означает di(s) дважды +polos полюс, что исключительно применимо к двухполюсным конструкциям, каковым и является резонансный трансформатор Николы Тесла с емкостной двухполюсной нагрузкой.
Внимательно изучив цели построения резонансного трансформатора Николы Тесла, невольно приходишь к выводу, что он был предназначен для передачи энергии на расстояние, но эксперимент был прерван, а потомкам остается догадываться о истинной цели этого чуда, конца 19 и начала 20 века. Не случайно Никола Тесла в своих записях оставил следующее изречение: — «Пусть будущее рассудит и оценит каждого по его трудам и достижениям. Настоящее принадлежит им, будущее, ради которого я работаю, принадлежит мне».
Резонансные элементы любого контура можно изменять в разных пределах и как с ними поступишь, так они и поведут себя. Можно увеличить индуктивность в этой конструкции и получить на поверхности сферы стримеры, коронарные разряды и даже молнии. Можно увеличить емкость и в режиме резонанса напряжений добиться максимальной отдачи сбалансированного электромагнитного поля. И все же Тесла был прав, когда отказался от металлического сердечника внутри повышающей катушки, ведь он вносил потери в том месте, где зарождалась электромагнитная волна.
Автор статьи повторил конструкцию трансформатора Тесла на частоте 7МГц. Параметры индуктивности и емкости сильно разнились, но результаты экспериментов привели к единственно правильному условию, когда ХL= -Хс стали соответствовать табличным данным (табл.1). Интересно то, что если уменьшать излучающую емкость, то для получения резонанса приходится увеличивать индуктивность. При этом, на краях излучателя и других неровностях, появляются стримеры (от англ. Streamer). Streamer, это тускло видимая, ионизация воздуха (свечение ионов), создаваемая полем диполя. Это и есть резонансный трансформатор Тесла, каким мы его привыкли видеть на просторах Интернета.
Проверка принципа действия диполя Тесла на практике.
Для проведения экспериментов с трансформатором Тесла над конструкцией не пришлось долго думать, здесь помог радиолюбительский опыт. В качестве излучателей вместо сферы и земли были взяты две гофрированные алюминиевые (вентиляционные) трубы диаметром 120мм и длиной по 250 мм. Удобство применения заключалось в том, что их можно растягивать или сжимать как витки катушки, тем самым, меняя емкость контура в целом и соответственно соотношение L/С. «Трубы – емкости» располагались горизонтально на бамбуковой палке с расстоянием 100мм. Катушка индуктивности L2 (30 мкГн) проводом 2 мм, была вынесена ниже оси цилиндров на 50 см. с тем, что бы не создавать вихревых токов в сфере излучателей. Еще лучше будет, если катушку вынести за один из излучателей, располагая ее на одной оси с ними, где эл. магнитное поле минимально и имеет форму «пустой воронки». Катушка связи L1 (1 виток, 2мм), обеспечивала связь с трансивером мощностью 40 вт. Образованный, этими элементами колебательный контур был настроен в режиме последовательного резонанса, где было соблюдено правило, а именно ХL = -Хс. Катушкой L1, соответственно было настроено согласование импровизированного диполя Тесла с фидером 50 Ом. Фидер длиной 5 метров для чистоты эксперимента был обеспечен с обоих сторон ферритовыми фильтрами.
Для сравнения испытывалось три антенны:
- диполь Тесла (L= 0.7м, КСВ=1,1),
- разрезной укороченный диполь Герца (L = 2х0,7м, удлинительная катушка, фидер 5 метров защищенный ферритовыми фильтрами КСВ=1,0),
- горизонтальный полуволновой диполь Герца (L = 19,3м, фидер защищен ферритовыми фильтрами КСВ=1,05).
На расстоянии 3 км. в черте города был включен передатчик с постоянной несущей сигнала.
Диполь Тесла (7 МГц) и укороченный диполь с удлиняющей катушкой, по очереди размещались возле кирпичного здания на расстоянии всего 2 метра, и на момент эксперимента находились в равных условиях на высоте (10-11м).
В режиме приема диполь Тесла превосходил укороченный диполь Герца на 2-3 балла (12-20 дБ) по шкале S-метра трансивера и более.
За тем вывешивался, за ранее настроенный, полуволновый диполь Герца. Высота подвеса 10-11 м. на расстоянии от стен в 15-20м.
По усилению диполь Тесла уступал полуволновому диполю Герца примерно на 1 балл (6-8дБ). Диаграммы направленности всех антенн совпадали. Стоит отметить, что полуволновый диполь был размещен не в идеальных условиях, а практика построения диполя Тесла требует новых навыков. Все антенны находились внутри двора (четыре здания), как в экранированном котле.
Общие выводы.
Рассматриваемый диполь Тесла на практике работает почти как полноценный полуволновый диполь Герца, он подчиняется принципам двойственности, что не идет в разрез с теорией антенн. Не смотря на свои сверх — малые размеры (0,01- 0,02λ), диполь Тесла осуществляет связь с пространством в виде емкостных пластин, сферы, цилиндров и пр.. Напряжение и ток в момент последовательного резонанса синфазны. Соответственно создают в пространстве, вокруг излучателя, синфазное поле Е и поле Н, что приводит к размышлению о том, что поле диполя Тесла в пределах излучателей уже сформировано и имеет «мини-сферу». Следует вспомнить, что у диполя Герца сферой считается то место, где поле Е и поле Н находятся в фазе, а именно на расстоянии 2-3 длины волны. Таким образом, диполь Тесла имеет все основания для практических экспериментов в радиолюбительской службе в диапазонах коротких, средних и особенно длинных волн. Думаю, что любителям длинноволновой связи (137кГц) стоит обратить на этот эксперимент особое внимание. Здесь имеется огромный потенциал проявить свою смекалку в усовершенствовании емкостного излучателя и подтвердить высказывание Г. Герца в том, что уровень излучения емкостного излучателя равен уровню излучения электрического диполя.
Примечание: Диполь Тесла относится к емкостным излучателям, не путать с полуволновым диполем Герца. Принципы их действия разнятся как, «водоплавающие от наземных», как катер от автомобиля, — мотор один, а движители разные.
UA9LBG. Сушко С.А.
Комментарии
Отзывы читателей — Скажите свое мнение!
Оставьте свое мнение
Отзывы читателей — Скажите свое мнение!
Источник
