Метод сечения и его польза


Метод сечений позволяет определить внутренние силы, которые возникают в стержне, находящемся в равновесии под действием внешней нагрузки.
Рассмотрим идеально упругий призматический стержень прямоугольного поперечного сечения (рис. 1.2, а).
Выделим внутри стержня какие-либо две частицы K и L, расположенные на бесконечно малом расстоянии друг от друга. Для большей наглядности предположим, что между этими частицами имеется некоторая пружинка, удерживающая их на определенном расстоянии друг от друга. Пусть натяжение пружинки равно нулю.
Приложим теперь к стержню растягивающую силу (рис. 1.2, б). Пусть в результате деформации стержня, частица K перейдет в положение , а частица L – в положение . Соединяющая эти частицы пружинка при этом растянется. После снятия внешней нагрузки частицы вернутся в первоначальное положение K и L благодаря усилию, которое возникло в пружинке. Сила, которая возникла между частицами (в пружинке) в результате деформации идеально упругого стержня, называются силой упругости или внутренней силой. Она может быть найдена методом сечений.
Этапы метода сечений
Метод сечений состоит из четырех последовательных этапов: разрезать, отбросить, заменить, уравновесить.
Разрежем стержень, находящийся в равновесии под действием некоторой системы сил (рис. 1.3, а) на две части плоскостью, перпендикулярной к его оси z.
Отбросим одну из частей стержня и рассмотрим оставленную часть.
Поскольку мы как бы разрезали бесчисленное множество пружинок, соединявших бесконечно близкие частицы тела, разделенного теперь на две части, в каждой точке поперечного сечения стержня необходимо приложить силы упругости, которые при деформации тела возникли между этими частицами. Иными словами, заменим действие отброшенной части внутренними силами (рис. 1.3, б).
Внутренние силы в методе сечений
Полученную бесконечную систему сил по правилам теоретической механики можно привести к центру тяжести поперечного сечения. В результате получим главный вектор R и главный момент M (рис. 1.3, в).
Разложим главный вектор и главный момент на составляющие по осям x, y (главные центральные оси) и z.
Получим 6 внутренних силовых факторов, возникающих в поперечном сечении стержня при его деформировании: три силы (рис. 1.3, г) и три момента (рис. 1.3, д).
Сила N – продольная сила
– поперечные силамы,
момент относительно оси z () – крутящий момент
моменты относительно осей x, y () – изгибающие моменты.
Запишем для оставленной части тела уравнения равновесия (уравновесим):
.
Из уравнений определяются внутренние усилия, возникающие в рассматриваемом поперечном сечении стержня.
Вычисление продольной и поперечных сил, крутящего и изгибающих моментов
продольная сила N равна сумме проекций всех сил (активных и реактивных), действующих на любую из частей рассеченного стержня, на ось z;
поперечные силы равны сумме проекций всех сил, действующих на любую из частей стержня, на оси x и y, соответственно;
крутящий момент равен сумме моментов всех сил, действующих на любую из частей стержня, относительно продольной оси z;
изгибающие моменты равны сумме моментов всех сил, действующих на любую из частей стержня, относительно осей x и y, соответственно.
Источник
Школа Стамо. www.stamoschool.com. Бесплатный Арткурс по основам рисунка
Мы с вами уже поднимали тему композиции и гармоничного расположении предметов на листе бумаги (холстекартине). Для тех, кто пропустил эту информацию, предлагаю вернуться и прочесть. Желательно зайти на сайт Школы и все по порядку изучить.
Итак, “Золотое сечение”. Думаю, это словосочетание слышали абсолютно все. Золотое сечение используется не только в живописи и графике, оно применяется в архитектуре, математике (потому что изначально это более математический подход к гармонии).
Чем больше я погружаюсь в эту тему, тем больше понимаю, как математический расчет часто применяется сухо в творчестве. Это к слову, когда мы говорили о пропорциях и схемах для изображения лица и фигуры человека. То есть, когда художники, а особенно начинающие, подстраивают натуру под схему, а не наоборот.
Важно понимать, что ЗС просто прикладывают (можно подобрать другое слово) к готовой картине великого мастера, а не мастер пишет картину по методу ЗС. Сейчас на просторах сети можно найти массу примеров работ, которые поделены на прямоугольники, квадраты, спирали, чтобы доказать на сколько точно авторы картин владели пифагоровским методом (хоть Пифагор номинально был первым, но фактически еще египтяне использовали эти расчеты).
Очень часто вы можете встретить фото картин Леонардо Да Винчи, с такими линиями как на фото ниже – это применение золотого сечения и пояснение правила.
Пример из сети
Для чего оно нужно? Для поиска идеального равновесия в работе. Всё предметы и персонажи, все цветовые пятна должны гармонировать друг с другом. Начинающие берут за основу схему и подстраивают работы под неё. Я же предлагаю эту гармонию искать внутри себя и нарушать правила. Я не склоняюсь утверждать, что золотое сечение не применимо. Наоборот, я за то чтобы изучить правила и знать потом, как их нарушать. А значит, что нас не ограничивает, то дает возможность больше проявить свободу творчества.
Но для того, чтобы знать, нужно разбираться и понимать, что именно мы будем нарушать)). Давайте поближе рассмотрим, что это за таинственные линии такие, которые сами создают гармонию.
Начнём с самого определения. Золотое сечение – это пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей или другими словами, меньший отрезок так относится к большему, как больший ко всему.
Отношение отрезков к друг другу. “а” относится к “b” , как “b” к “с”
Эти соотношения сторон могут быть применены в разных сферах. Не только внутри картины (сюжета), но и в архитектуре зданий, природе:
Золотые отрезки в природе
Золотые пропорции можно наблюдать абсолютно везде. Но, знание этих правил не диктует нам схемы, от которых нельзя отталкиваться, они лишь подсказывают и направляют. Это значит, что вам не нужно, прежде чем начать рисовать, взять линейку и расчертить лист на отрезки согласно данного правила, а потом подстраивать все под линии и никуда дальше не двигаться. Золотое сечение можно и нужно использовать, если вы знаете зачем.
Плоскоть, согласно ЗС, делится по такому же принципу: меньшая площадь к большей, также как большая к общей. Так появляется знаменитая Золотая спираль:
Площадь квадрата “В” относится к площади квадрата “А”, также как площадь “С” к порщади”В” и тд.
Такие квадраты образуются, когда мы делим периметр согласно золотых отрезков. Таким образом, любой лист, любого размера можно поделить и нарисовать такую спираль.
Фото-пример
Если же мы делим только геометрические стороны листа, то достаточно объединить противоположные точки. Я бы не хотела углубляться в построение схем, как правильно их строить, какие отрезки брать за основу, поэтому сразу показываю примеры. Если вам нужны более детальные пояснения, то сообщите об этом в комментариях.
Наши отрезки образуют точки 1,2,3 и 4
Расположение объектов (персонажей, предметов, цветовых пятен) в точках 1-4 привлекут внимание зрителей. Такое положение вещей считается полной гармонией и не вызовет зрительного дисбаланса.
Пример из сети
Если провести диагонали, то можно найти ещё одно правило гармонии-диагональное:
Схема из сети
Повторюсь, не обязательно брать линейку и измерять. Достаточно запомнить приблизительное расположение линий и отталкиваться от них на глаз.
Есть другое правило: симметрии. Если его использовать в своих работах, то можно либо допустить ошибку, либо наоборот создать что-то необычное. Например, когда в картине горизонт проходит посредине листа, то часто это выдают за ошибку. Потому что нет глубины идеи, что именно хотел донести автор работы. На чем конкретно сделан акцент.
То есть, если мы хотим изобразить и погрузить зрителя в просторы полей, рек, озер, морей и тд, то линию горизонта мы поднимаем выше центральной геометрической точки листа.
Фото-пример
Если мы хотим изобразить небо, акцентировать внимание на облаках или красоты заката, то линию горизонта нужно опустить ниже.
Фото-пример
Все это мы делаем исходя из гармонии, зная основные правила композиции.
Основная ошибка гласит: если разместить линию горизонта по центру листа, то теряется гармония. Но, мы можем нарушать правила. Например, у нас задумка изобразить зеркальность поверхности. Допустим перед нами здание, а перед зданием гладкое озеро и такое гладкое, что здание отражается в нем без всяких искажений. Тогда наш посыл будет в акценте на зеркальности, отражении, поэтому и расположение горизонта вполне оправдано.
Фото-пример. Тажд-Махал
Также, такой метод симметрии листа можно использовать, если мы хотим изобразить абсолютно противоположные, но равные по смыслу миры.
Фото-пример вертикальной симметрии
Фантазия на этом не заканчивается. Можно творить все, что захочется. Важна задумка. Но если мы хотим сделать работу по классическому варианту, то, конечно, нужно прислушаться к правилам и рисовать горизонт там, где он лучше всего подчеркнет вашу идею.
Завышенный горизонт
На последок еще такое понятие как “динамическая симметрия“. Она создаёт более “собранную” композицию, объединяет все элементы внутри работы и интересно может смотреться в любых направлениях: фото, картина, скульптура:
Динамическая симметрия
А вот фото-пример:
Повторяющиеся элементы
Друзья, данная статья лишь показывает разнообразие композиционных подходов. Помимо Золотого сечения мы рассмотрим и другие, но смысл творчества всегда останется : правила есть правила, но свободу проявления творческой души никто не отменял. Не нужно подстраивать себя под правила, нужно правила подстроить под себя. Тогда ваши картины будут уникальными.
Желаю вдохновения и новых творческих идей!
Источник
Для расчетов деталей машин и сооружений на прочность необходимо знать внутренние силы упругости, возникающие в результате действия приложенных к деталям внешних сил.
В теоретической механике мы познакомились с понятием метода сечений. Этот метод широко применяется в сопротивлении материалов для определения внутренних сил, поэтому рассмотрим его подробно. Напомним, что всякое тело, в том числе деталь машины или сооружения, можно полагать системой материальных точек.
В теоретической механике имеют дело с неизменяемыми системами; в сопротивлении материалов рассматриваются изменяемые (деформируемые) системы материальных точек.
Метод сечений заключается в том, что тело мысленно рассекается плоскостью на две части, любая из которых отбрасывается, а взамен нее к сечению оставшейся части прикладываются внутренние силы, действовавшие до разреза. Оставленная часть рассматривается как самостоятельное тело, находящееся в равновесии под действием внешних и приложенных к сечению внутренних сил.
Очевидно, что, согласно третьему закону Ньютона (аксиома взаимодействия), внутренние силы, действующие в сечении оставшейся и отброшенной частей тела, равны по модулю, но противоположны по направлению. Поэтому, рассматривая равновесие любой из двух частей рассеченного тела, мы получим одно и то же значение внутренних сил, однако выгоднее рассматривать ту часть тела, для которой уравнения равновесия проще.
В соответствии с принятым допущением о непрерывности материала тела мы можем утверждать, что внутренние силы, возникающие в теле, представляют собой силы, равномерно или неравномерно распределенные по сечению.
Применяя к оставленной части тела условия равновесия, мы не сможем найти закон распределения внутренних сил по сечению, но сможем определить статические эквиваленты этих сил.
Так как основным расчетным объектом в сопротивлении материалов является брус и чаще всего нас будут интересовать внутренние силы в его поперечном сечении, то рассмотрим, каковы будут статические эквиваленты внутренних сил в поперечном сечении бруса.
Рассечем брус (рис. 1.3) поперечным сечением а — а и рассмотрим равновесие его левой части.

Рис. 1.3
Если внешние силы, действующие на брус, лежат в одной плоскости, то в общем случае статическим эквивалентом внутренних сил, действующих в сечении а — а, будут главный вектор Fm, приложенный в центре тяжести сечения, и главный момент МТЛ — МИ, уравновешивающие плоскую систему внешних сил, приложенных к оставленной части бруса.
Разложим главный вектор на составляющую N, направленную вдоль оси бруса, и составляющую Q, перпендикулярную этой оси, то есть лежащую в плоскости поперечного сечения. Эти составляющие главного вектора вместе с главным моментом назовем внутренними силовыми факторами, действующими в сечении бруса. Составляющую N назовем продольной силой, составляющую Q — поперечной силой, а пару сил с моментом Мк — изгибающим моментом.
Для определения указанных трех внутренних силовых факторов статика дает три уравнения равновесия оставленной части бруса, а именно:

(ось z всегда направляем по оси бруса).
Если внешние силы, действующие на брус, не лежат в одной плоскости, то есть представляют собой пространственную систему сил, то в общем случае в поперечном сечении бруса возникают шесть внутренних силовых факторов (рис. 1.4), для определения которых статика дает шесть уравнений равновесия оставленной части бруса, а именно:


Рис. 1.4
Шесть внутренних силовых факторов, возникающих в поперечном сечении бруса в самом общем случае, носят следующие названия: N — продольная сила, Qx, Qy— поперечные силы, Мк — крутящий момент, Мш, Миу— изгибающие моменты.
При разных деформациях в поперечном сечении бруса возникают различные внутренние силовые факторы. Рассмотрим частные случаи.
- 1. В сечении возникает только продольная сила N. В таком случае это деформация растяжения (если сила N направлена от сечения) или деформация сжатия (если сила N направлена к сечению).
- 2. В сечении возникает только поперечная сила Q. В таком случае это деформация сдвига.
- 3. В сечении возникает только крутящий момент Мк. В таком случае это деформация кручения.
- 4. В сечении возникает только изгибающий момент Мн. В таком случае это деформация чистого изгиба. Если в сечении одновременно возникает изгибающий момент Мн и поперечная сила Q, то изгиб называют поперечным.
- 5. В сечении одновременно возникает несколько внутренних силовых факторов (например, изгибающий и крутящий моменты или изгибаюший момент и продольная сила). В этих случаях имеет место сочетание основных деформаций.
Наряду с понятием деформации одним из основных понятий сопротивления материалов является напряжение. Напряжение характеризует интенсивность внутренних сил, действующих в сечении.
Рассмотрим какой-либо произвольно нагруженный брус и применим к нему метод сечений (рис. 1.5). Выделим в сечении бесконечно малый элемент площади dA (что мы имеем право делать, так как считаем материал непрерывным). Ввиду малости этого элемента можно считать, что в его пределах внутренние силы, приложенные в различных точках, одинаковы по модулю и направлению и, следовательно, представляют собой систему параллельных сил. Равнодействующую этой системы обозначим dF. Разделив dF на площадь элементарной площадки dA, определим интенсивность внутренних сил, то есть напряжение р в точках элементарной площадки dA:


Рис. 1.5
Таким образом, напряжение есть внутренняя сила, отнесенная к единице площади сечения. Напряжение есть величина векторная. Единица напряжения:

Поскольку эта единица напряжения очень мала, то мы будем применять более крупную кратную единицу, а именно мегапаскаль (МПа): 1 МПа = 106Па = 1 Н/мм2. Таким образом, числовые значения напряжения, выраженного в МПа и Н/мм2, совпадают.
Разложим вектор напряжения р на две составляющие: о — перпендикулярную плоскости сечения и т — лежащую в плоскости сечения (рис. 1.5). Эти составляющие назовем соответственно нормальным (а) и касательным (т) напряжением.
Так как угол между нормальным и касательным напряжениями всегда равен 90°, то модуль полного напряженияр определится по формуле

Разложение полного напряжения на нормальное и касательное имеет вполне определенный физический смысл. Как мы убедимся в дальнейшем, в поперечном сечении бруса при растяжении, сжатии и чистом изгибе действуют только нормальные напряжения, а при сдвиге и кручении — только касательные напряжения.
В заключение настоящей главы рассмотрим гипотезу, которая носит название принцип независимости действия сил и формулируется так: при действии на тело нескольких нагрузок внутренние силы, напряжения, перемещения и деформации в любом месте могут быть определены как сумма этих величин, найденных от каждой нагрузки в отдельности.
Пользуясь принципом независимости действия сил, мы, начав с изучения простейших основных деформаций, когда в поперечных сечениях бруса действуют только нормальные или только касательные напряжения, в дальнейшем перейдем к изучению более сложных основных деформаций, когда в поперечном сечении действуют и те и другие напряжения, а затем рассмотрим случаи сочетания основных деформаций, что иногда называют сложным сопротивлением.
Заметим, что принцип независимости действия сил применим только для конструкций, деформации которых малы по сравнению с размерами и пропорциональны действующим нагрузкам.
Источник
Метод
сечений
позволяет определить внутренние силы,
которые возникают в стержне, находящемся
в равновесии под действием внешней
нагрузки.
ЭТАПЫ
МЕТОДА СЕЧЕНИЙ
Метод
сечений состоит
из четырех последовательных
этапов: разрезать,
отбросить, заменить, уравновесить.
Разрежем стержень,
находящийся в равновесии под действием
некоторой системы сил ![]() (рис.
(рис.
1.3, а) на две части плоскостью,
перпендикулярной к его оси z.
Отбросим одну
из частей стержня и рассмотрим оставленную
часть.
Поскольку
мы как бы разрезали бесчисленное
множество пружинок, соединявших
бесконечно близкие частицы тела,
разделенного теперь на две части, в
каждой точке поперечного сечения стержня
необходимо приложить силы упругости,
которые при деформации тела возникли
между этими частицами. Иными
словами, заменим действие
отброшенной части внутренними
силами(рис. 1.3, б).
ВНУТРЕННИЕ
СИЛЫ В МЕТОДЕ СЕЧЕНИЙ
Полученную
бесконечную систему сил по правилам
теоретической механики можно привести
к центру тяжести поперечного сечения.
В результате получим главный вектор R
и главный момент M (рис. 1.3, в).
Разложим
главный вектор и главный момент на
составляющие по осям x, y (главные
центральные оси) и z.
Получим
6 внутренних
силовых факторов,
возникающих в поперечном сечении стержня
при его деформировании: три силы ![]() (рис.
(рис.
1.3, г) и три момента![]() (рис.
(рис.
1.3, д).
Сила
N – продольная сила
![]() –поперечные силамы,
–поперечные силамы,
момент
относительно оси z (![]() )
)
– крутящий момент
моменты
относительно осей x, y (![]() )
)
– изгибающие моменты.
Запишем
для оставленной части тела уравнения
равновесия (уравновесим):
![]() .
.
Из
уравнений определяются внутренние
усилия, возникающие в рассматриваемом
поперечном сечении стержня.
12.Метод
сечений. Понятие о внутренних усилиях.
Простые и сложные деформации.
Деформации
рассматриваемого тела (элементов
конструкции) возникают от приложения
внешней силы. При этом изменяются
расстояния между частицами тела, что в
свою очередь приводит к изменению сил
взаимного притяжения между ними. Отсюда,
как следствие, возникают внутренние
усилия. При этом внутренние усилия
определяются универсальным методом
сечений (или метод разреза).Простые
и сложные деформации. Использование
принципа суперпозиции.
Деформация
бруса называется простой, если в его
поперечных сечениях возникает только
один из вышеперечисленных внутренних
силовых факторов. Здесь и далее силовым
фактором будем называть любую силу или
момент.
Лемма.
Если брус прямой, то любая внешняя
нагрузка (сложная нагрузка) может быть
разложена на составляющие (простые
нагрузки), каждая из которых вызывает
одну простую деформацию (один внутренний
силовой фактор в любом сечении бруса).
Читателю
предлагается самостоятельно доказать
лемму для любого частного случая
нагружения бруса (подсказка: в ряде
случаев требуется вводить фиктивные
самоуравновешенные нагрузки).
Существуют
четыре простые деформации прямого
бруса:
–
чистое растяжение – сжатие ( N ≠ 0, Qy=
Qz=
Mx=
My=
Mz=0
);
–
чистый сдвиг ( Qy или
Qz ≠
0, N = Mx=
My=
Mz=
0 );
–
чистое кручение ( Mx ≠
0, N = Qy=
Qz=
My=
Mz=
0 );
–
чистый изгиб ( My или
Mz ≠
0, N = Qy=
Qz=
Mx =
0 ).
На
основании леммы и принципа суперпозиции
задачи сопротивления материалов можно
решать в следующей последовательности:
–
в соответствии с леммой сложную нагрузку
разложить на простые составляющие;
–
решить полученные задачи о простых
деформациях бруса;
–
просуммировать найденные результаты
(с учётом векторного характера параметров
напряженно-деформированного состояния).
В соответствии с принципом суперпозиции
это будет искомое решение задачи.
13. Понятие
о напряжённых внутренних силах. Связь
между напряжениями и внутренними
силами.
Механическое
напряжение
— это мера внутренних сил, возникающих
в деформируемом теле, под влиянием
различных факторов. Механическое
напряжение в точке тела определяется
как отношение внутренней силы к единице
площади в данной точке рассматриваемого
сечения.
Напряжения
являются результатом взаимодействия
частиц тела при его нагружении. Внешние
силы стремятся изменить взаимное
расположение частиц, а возникающие при
этом напряжения препятствуют смещению
частиц, ограничивая его в большинстве
случаев некоторой малой величиной.
Q
— механическое напряжение.
F
— сила, возникшая в теле при деформации.
S
— площадь.
Различают
две составляющие вектора механического
напряжения:
Нормальное
механическое напряжение — приложено
на единичную площадку сечения, по нормали
к сечению (обозначается ).
Касательное
механическое напряжение — приложено
на единичную площадку сечения, в плоскости
сечения по касательной (обозначается
).
Совокупность
напряжений, действующих по различным
площадкам, проведенным через данную
точку, называется напряженным состоянием
в точке.
В
Международной системе единиц (СИ)
механическое напряжение измеряется в
паскалях.
14.Центральное
растяжение и сжатие. Внутренние усилия
. Напряжения. Условия прочности.
Центральным
растяжением (или центральным сжатием)
называется такой вид деформации, при
котором в поперечном сечении бруса
возникает только продольная сила
(растягивающая или сжимающая), а все
остальные внутренние усилия равны нулю.
Иногда центральное растяжение (или
центральное сжатие) кратко называют
растяжением (или сжатием) .
Правило
знаков
Растягивающие
продольные усилия принято считать
положительными, а сжимающие —
отрицательными.
Рассмотрим
прямолинейный брус (стержень), нагруженный
силой F
Растяжение
стержня
Определим
внутренние усилия в поперечных сечениях
стержня методом сечения.
Напряжение
— это внутренне усилие N, приходящее на
единицу площади A. Формула для нормальных
напряжений σ при растяжении
=

Так
как поперечная сила при центральном
растяжении-сжатии равна нулю2, то и
касательное напряжение =0.
Условие
прочности при растяжении-сжатии
max![]() =
=
|
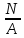
|
![]() [
[![]() ]
]
15.
Центральное растяжение и сжатие
. Условие прочности. Три типа задач при
центральном растяжении (сжатии).Условие
прочности позволяет решать три типа
задач:
1. Проверка
прочности (проверочный расчет)
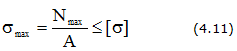
2. Подбор
сечения (проектировочный расчет)

3. Определение
грузоподъемности (допускаемой нагрузки)
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
10.02.20161.72 Mб11referat_turbaza.docx
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
